网赌输20万，现在走头无路，该怎么办？

我一个朋友也是和你一样的遭遇，刚开始玩的时候，还赢了一些，后面慢慢的越套越多

失去了理智，各种平台贷款，贷的越来越多，窟窿越来越大

对生活充满的失望

因为我是做技术的，在安全这方面做了很久了

他找到我，问我有没有办法给他挽回损失，利用技术手段

这个东西说实话，得看具体情况，平台要是跑路了，我也没辙，所幸平台还在

然后设计了一下思路就开始开始给他整

因为他的资金详情都在平台那边的服务器和数据库上面

我看了下，服务器搭建在越南

安全方面做的不是太好，有一些不易察觉的漏洞存在

然后利用工具开始扫描漏洞

经过扫描，扫描到了后台未授权访问的链接、备份文件、编辑器、敏感信息等。

如果你是老司机，后台登陆的网址看多了，甚至不用御剑什么的工具跑，就能直接猜到。

一般碰到下面这种情况，可采用fuzz大法。一层一层fuzz，尝试寻找可利用的信息。

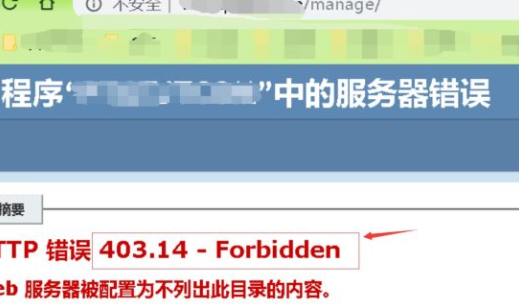
经过扫描发现是Java站，且链接是.do结尾，但struct2工具试了下没成功。

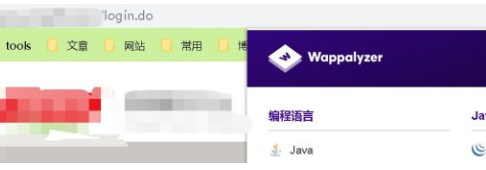
然后看到登陆界面

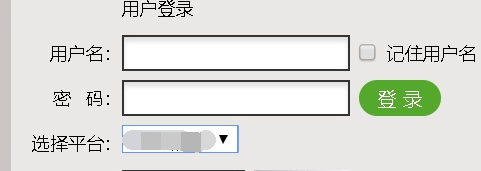
首先扫到了一个services服务路径

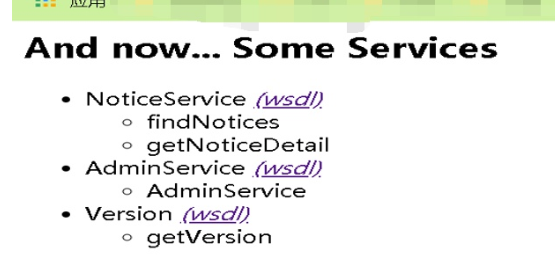
知道了Apache Axis组件的版本信息

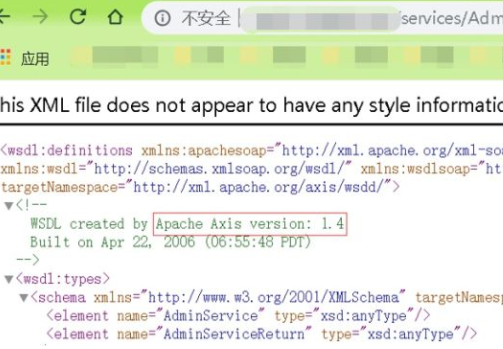
然后马上想到这个组件当时刚爆出一个RCE漏洞

poc链接：https://github.com/KibodWapon/Axis-1.4-RCE-Poc

还扫出了一个ckfinder编辑器

经过一些操作之后，拿到了权限，修改了资金数据

虽然资金数据修改了，但是提现的时候，出了问题，后来找到原因是因为有个权限没修改，

经过修改之后，帮他挽回了损失

其实，他这个还属于运气好，平台没有跑路，包括平台安全方面做的不是太好

如果哪个环节有一些问题的话，肯定是没有那么轻松容易就挽回损失的

简单说到这里吧

如果你也是在哪个平台扔了一堆钱进去，现在难受的一匹，最好先停手，然后找个懂技术的给你看下，不然，等一段儿时间过去了，你想挽回损失也难了

有不懂的问题也可以找我交流，参考下图

open HolKernel boolLib bossLib Parse;

open arithmeticTheory integerTheory integer_wordTheory wordsTheory listTheory;

open pred_setTheory finite_mapTheory;

open settingsTheory miscTheory llairTheory;

new_theory "llair_prop";

numLib.prefer_num ();

Theorem signed2unsigned_fits:

0 < n ∧ ifits i n ⇒ ifits (&signed2unsigned i n) (n + 1)

Proof

rw [signed2unsigned_def, ifits_def]

>- (

`?j. i = -&j` by intLib.COOPER_TAC >>

rw [] >> fs [] >>

rfs [EXP_SUB] >>

`j ≤ 2 ** n` by intLib.COOPER_TAC >>

rw [INT_SUB, GSYM int_sub])

>- (

`?j. i = &j` by intLib.COOPER_TAC >>

rw [] >> fs [] >>

rw [INT_SUB, GSYM int_sub] >>

rfs [EXP_SUB] >>

intLib.COOPER_TAC)

QED

Theorem i2n_n2i:

∀n size. 0 < size ⇒ (nfits n size ⇔ (i2n (n2i n size) = n))

Proof

rw [nfits_def, n2i_def, i2n_def, signed2unsigned_def] >> rw []

>- intLib.COOPER_TAC

>- (

`2 ** size ≤ n` by intLib.COOPER_TAC >> simp [INT_SUB] >>

Cases_on `n = 0` >> fs [] >>

`n - 2 ** size < n` suffices_by intLib.COOPER_TAC >>

irule SUB_LESS >> simp [])

>- (

`2 ** (size - 1) < 2 ** size` suffices_by intLib.COOPER_TAC >>

fs [])

QED

Theorem n2i_i2n:

∀i size. 0 < size ⇒ (ifits i size ⇔ (n2i (i2n (IntV i size)) size) = IntV i size)

Proof

rw [ifits_def, n2i_def, i2n_def, signed2unsigned_def] >> rw [] >> fs []

>- (

eq_tac >> rw []

>- (

simp [intLib.COOPER_PROVE ``∀(x:int) y z. x - y = z ⇔ x = y + z``] >>

`2 ** (size - 1) < 2 ** size` suffices_by intLib.COOPER_TAC >>

fs [INT_OF_NUM])

>- (

fs [intLib.COOPER_PROVE ``∀(x:int) y z. x - y = z ⇔ x = y + z``] >>

fs [INT_OF_NUM] >>

`∃j. i = -j` by intLib.COOPER_TAC >> rw [] >> fs [] >>

qpat_x_assum `_ ≤ Num _` mp_tac >>

fs [GSYM INT_OF_NUM] >>

ASM_REWRITE_TAC [GSYM INT_LE] >> rw [] >>

`2 ** size = 2 * 2 ** (size - 1)` by rw [GSYM EXP, ADD1] >> fs [] >>

intLib.COOPER_TAC)

>- intLib.COOPER_TAC)

>- (

eq_tac >> rw []

>- intLib.COOPER_TAC

>- intLib.COOPER_TAC >>

`0 ≤ i` by intLib.COOPER_TAC >>

fs [GSYM INT_OF_NUM] >>

`&(2 ** size) = 0` by intLib.COOPER_TAC >>

fs [])

>- (

eq_tac >> rw []

>- (

`2 ** size = 2 * 2 ** (size - 1)` by rw [GSYM EXP, ADD1] >> fs [] >>

intLib.COOPER_TAC)

>- intLib.COOPER_TAC

>- intLib.COOPER_TAC)

>- intLib.COOPER_TAC

QED

Theorem w2n_signed2unsigned:

∀w. w2n (w : 'a word) = signed2unsigned (w2i w) (dimindex (:'a))

Proof

rw [signed2unsigned_def] >> Cases_on `w` >> fs []

>- (

`INT_MIN (:α) ≤ n`

by (

fs [w2i_def] >> rw [] >>

BasicProvers.EVERY_CASE_TAC >> fs [word_msb_n2w_numeric] >>

rfs []) >>

rw [w2i_n2w_neg, dimword_def, int_arithTheory.INT_NUM_SUB])

>- (

`n < INT_MIN (:'a)`

by (

fs [w2i_def] >> rw [] >>

BasicProvers.EVERY_CASE_TAC >> fs [word_msb_n2w_numeric] >>

rfs []) >>

rw [w2i_n2w_pos])

QED

Theorem w2n_i2n:

∀w. w2n (w : 'a word) = i2n (IntV (w2i w) (dimindex (:'a)))

Proof

rw [i2n_def] >> metis_tac [w2n_signed2unsigned]

QED

Theorem w2i_n2w:

∀n. n < dimword (:'a) ⇒ IntV (w2i (n2w n : 'a word)) (dimindex (:'a)) = n2i n (dimindex (:'a))

Proof

rw [n2i_def]

>- (

qspec_then `n` mp_tac w2i_n2w_neg >>

fs [dimword_def, INT_MIN_def] >> rw [GSYM INT_SUB])

>- (irule w2i_n2w_pos >> rw [INT_MIN_def])

QED

Theorem eval_exp_ignores_lem:

∀s1 e v. eval_exp s1 e v ⇒ ∀s2. s1.locals = s2.locals ∧ s1.glob_addrs = s2.glob_addrs ⇒ eval_exp s2 e v

Proof

ho_match_mp_tac eval_exp_ind >>

rw [] >> simp [Once eval_exp_cases] >>

TRY (qexists_tac `vals` >> rw [] >> fs [LIST_REL_EL_EQN] >> NO_TAC) >>

TRY (fs [LIST_REL_EL_EQN] >> NO_TAC) >>

metis_tac []

QED